Une oscillation entretenue

On suppose un masse retenue par un ressort et possée sur un tapis roulant. Le tapis déplace la masse jusqu'à ce que les frottements ne suffisent plus à la retenir et que le ressort la rappelle. Puis le cycle recommence.

Ce mouvement est régit par l'équation suivante :

$$\frac{{\partial}^2 x}{\partial {t}^2} + \omega^2 \, x + \alpha \, sign(\frac{\partial x}{\partial t} -v) = 0$$

avec $\omega$ et $\alpha$ des constantes que l'on fixe à 1 et v la vitesse du tapis roulant que l'on fixe à 2.

• écrire le système d'équations différentielles d'ordre 1 équivalent à l'équation ci-dessus (on prend x₁=x et $x_2=\frac{\partial x}{\partial t}$).
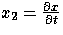• calculer les courbes sur l'intervale [0 20] pour les conditions initiales

  $$\begin{array} {rcl} \circ \quad (x_1,x_2)(0) &=& (0.2, 0.8) ... ... (0.5, 0.5) \\ \circ \quad (x_1,x_2)(0) &=& (-2, 8) \end{array}$$ (4)

• tracer dans un repère orthonormé les courbes correspondant à chacune des solutions (on trace x₂ en fonction de x₁).
• dessiner à l'aide de la fonction quiver le champs vectoriel correspondant à la fonction ${\bold{f}}=(f_1,f_2)=(\frac{\partial x_1}{\partial t}, \frac{\partial x_2}{\partial t})$ sur le carré $[-6,6]\times[-6,6]$.
• superposer à ce graphe, les courbes tracées précédemment.