Cette leçon a 3 effets positifs :

• manipuler des bases de sous-espaces
• mélanger les dérivées partielles et les vecteurs
• trouver un algorithme plus performant que la méthode du gradiant pour résoudre $A \, {\bf x} = {\bf b}$

Méthode du gradient conjugué

On a vu que dans la méthode du gradiant on peut calculer le µ optimal pour aller directement au minimum de la fonctionnelle $J$ dans le long de la ligne ${\bf x}^k \; + µ \, \nabla J({\bf x}^k)$ avec µ qui varie de $- \infty$ à $+ \infty$ (cf ma33).

On a aussi vu que si on a le µ optimal, alors la plus forte pente suivante, $\nabla J ({\bf x}^{k+1})$, sera orthogonale à la pente qui définie la droite sur laquelle on cherche µ. On a donc

$$\nabla J ({\bf x}^{k+1})^T \, . \, \nabla J ({\bf x}^k) = 0$$

C'est bien car cela veut dire que le minimum suivant, ${\bf x}^{k+2}$, sera le minimum de l'espace généré par $\nabla J ({\bf x}^{k+1})$ et $\nabla J ({\bf x}^k)$ (ce qui est mieux que d'être seulement le minimum le long d'une ligne).

Malheureusement rien me dit que ${\bf x}^{k+3}$ ne sera pas calulé le long de notre première direction, $\nabla J({\bf x}^k)$. On a vu dans le cas du gradiant sans recherche du µ optimal qu'on peut osciller entre 2 valeurs. Cela n'est pas possible avec le µ optimal mais on peut tourner en rond sur quelques valeurs.

Même si on ne tourne pas en rond et qu'on converge est il probable qu'on cherche à nouveau un minimum dans une partie de l'espace $ℝ^n$ qu'on a déjà explorée.

Une recherche optimal du minimum d'une fonction convexe dans un espace $ℝ^n$ ne devrait pas prendre plus de $n$ itération si on est toujours capable de caluler le µ optimal dans la direction choisie. Pour s'en convaincre il suffit de choisir comme directions les vecteurs de la base de notre espace $ℝ^n$. Une fois qu'on a trouvé le minimum dans toutes les directions de la base, on a le minimum global. Il n'y a plus aucune direction possible de recherche qui ne serait pas la combinaison linéaire des vecteurs déjà utilisés.

Cas 2D

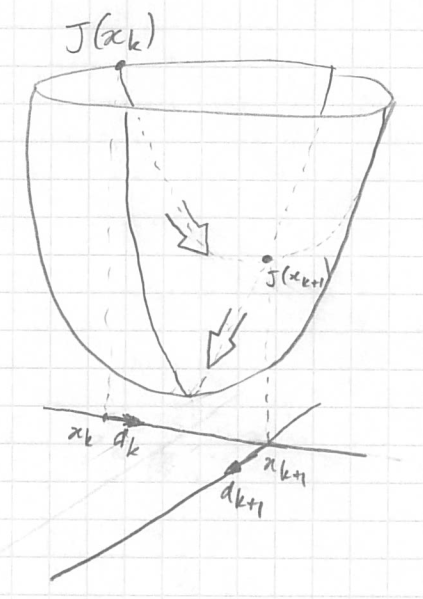
Si on cherche le point ${\bf x} = (x_1, x_2)$ qui minimise $J({\bf x})$ (convexe) et qu'on sait calculer le µ optimal de notre méthode de gradient, alors on trouve le minimum globale en 2 itérations au maximum. Mais on prend un µ trop grand qui nous fasse passer au dessus du minimum global, alors à la prochaine itération la plus grande pente sera exactement l'opposée de celle qu'on vient d'utiliser et on oscillera. Sur le dessin on voit bien qu'on trouve le minimum global en 2 itérations mais on se dit que c'est un coup de chance et d'ailleurs est-ce vraiment en 2 itérations puisqu'il est écrit ${\bf x}^k$ ? C'est toute la limite d'un dessin qui veut expliquer ce qui se passe dans $ℝ^n$ à des humains habitués à $ℝ^3$ (cf cette vidéo sur la 4e dimension en dehors du cours).

Générer une base de $ℝ^n$

Si on veut trouver notre minimum global en $n$ itération au maximum, il faut que nos directions ne soit pas redondante et donc que les $n$ premières directions génèrent $ℝ^n$ ou forment une base de $ℝ^n$.

Il faut donc que la nouvelle direction ${\bf d}^k$ soit orthogonales à toutes les directions précédentes ou qu'elle permette de trouver une base qui génère un espace de dimension $k+1$ (on commence avec ${\bf d}^0$).

Est-ce possible ?

Le cas $A {\bf x} = {\bf b}$

Dans ce cas la fonctionnelle à minimiser est

$$ J({\bf x}) = \frac{1}{2} \, {\bf x}^T \, A \, {\bf x} - {\bf b}\, . {\bf x} $$

et son gradient est $\nabla J({\bf x}) = A \; {\bf x} - {\bf b}$ si A est symétrique.

On sait que si on calcule ${\bf x}^k$ comme avant on a seulement d'orthogonalité de deux directions successives. Cela arrive lorsque µ est choisi pour minimiser $J$ le long de la droite de direction $\nabla J({\bf x}^k)$.

Que se passe-t-il si ${\bf x}^{k+1}$ minimise $J$ dans l'espace ${\bf G_k}$ généré par toutes les directions précédentes ?

$$ J({\bf x}^{k+1}) = \min_{\bf v \in G_k} J({\bf x}^k + {\bf v}) $$ avec ${\bf G_k} = span\{{\bf d}^0, {\bf d}^1,\dots, {\bf d}^k\} = \left\{ {\bf v} = \sum_{i=0}^{k} \alpha_i \, {\bf d}^i \quad \forall \alpha_i \in ℝ \right\}$.

Alors toutes les dérivées partielles par rapport aux vecteurs de ${\bf G_k}$ sont nulles (tout comme $\partial J / \partial x$ et $\partial J / \partial y$ sont nulles au minumum de J dans le dessin ci-dessus). Vectoriellement cela s'écrit ainsi :

$$ \nabla J({\bf x}^{k+1}) \, . \, {\bf w} = 0 \quad \forall {\bf w} \in {\bf G_k} \qquad (0) $$

ce qui se vérifie facilement si ${\bf w}$ est un des vecteurs de la base :

$$ \nabla J({\bf x}^{k+1}) \, . \, {\bf e}_i = \begin{bmatrix} \partial J / \partial x_{1} \\ \partial J / \partial x_{2} \\ \vdots \\ \partial J / \partial x_{i} \\ \vdots \\ \partial J / \partial x_{n} \\ \end{bmatrix} \, . \, \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \\ \end{bmatrix} = \frac{\partial J}{\partial x_i}({\bf x}^{k+1}) $$

On note que dire la dérivée partielle de $J$ dans une direction ${\bf w}$ de ${\bf G_k}$ est nulle, revient à dire que $\nabla J({\bf x}^{k+1})$ est orthogonal à ${\bf w}$ (ou nul si $\nabla J({\bf x}^{k+1})$ la même dimension que ${\bf G_k}$).

Générons les directions ${\bf d}^i$

Ainsi notre formule itérative devient :

$$ {\bf x}^{k+1} = {\bf x}^k + µ^k\, {\bf d}^k $$

Pour calculer les ${\bf d}^k$ on utilise la formule qui nous dit que les dérivées partielles de $J$ par rapport à un vecteur ${\bf w \in G_k}$ sont nulles. Et comme les directions ${\bf d}^i$ génèrent l'espace ${\bf G_k}$ il suffit que les dérivées partielles de $J$ par rapport à tous les ${\bf d}^i$ soient nulles :

$$ \nabla J({\bf x}^{k+1}) \, . \, {\bf d}^i = 0 \quad \forall i \le k \qquad (1) $$

On déroule les calculs

$$ \begin{align} (A\, {\bf x}^{k+1} - b) \, . \, {\bf d}^i &= 0 \quad \forall i \le k \\ (A\, ({\bf x}^{k} + µ^k \, {\bf d}^k) - b) \, . \, {\bf d}^i &= 0 \quad \forall i \le k \\ (A\, {\bf x}^{k} - b) \, . \, {\bf d}^i + µ^k \, A \, {\bf d}^k \, . \, {\bf d}^i &= 0 \quad \forall i \le k \\ \nabla J({\bf x}^{k}) \, . \, {\bf d}^i + µ^k \, A \, {\bf d}^k \, . \, {\bf d}^i &= 0 \quad \forall i \le k \\ \end{align} $$

Si $i < k$ alors le premier terme est nul ce qui donne

$$ A \, {\bf d}^k \, . \, {\bf d}^i = 0 \quad \forall i < k \qquad (2) $$

Comme A est symétrique, on a aussi $A \, {\bf d}^i \, . \, {\bf d}^k = 0 \quad \forall i < k\quad$ ($\sum_{m=1}^N \sum_{n=1}^N a_{m,n}\, d^i_n\, d^k_m = \sum_{n=1}^N \sum_{m=1}^N a_{n,m}\, d^k_m\, d^i_n$).

Ainsi on a des conditions pour construire la nouvelle direction ${\bf d}^k$.

On suppose que la nouvelle direction est le gradiant + une correction qui est une combinaison linéaire des directions précédantes : $$ {\bf d}^k = - \nabla J({\bf x}^k) + \sum_{j=0}^{k-1} β_j {\bf d}^j $$ alors l'équation (2) devient $$ A \, \left( - \nabla J({\bf x}^k) + \sum_{j=0}^{k-1} β_j {\bf d}^j \right) . {\bf d}^i = 0 \quad \forall i < k $$ La somme va faire apparaître des $A\, {\bf d}^j {\bf d}^i$ qui sont tous nul d'après (2) et sa version symétrique sauf $A\, {\bf d}^i {\bf d}^i$. Donc

$$ β_i = \frac{A\, \nabla J({\bf x}^k) \, . \, {\bf d}^i}{A\, {\bf d}^i \, . \, {\bf d}^i} $$

et ainsi $$ {\bf d}^k = - \nabla J({\bf x}^k) + \sum_{i=0}^{k-1} \frac{A\, \nabla J({\bf x}^k) \, . \, {\bf d}^i} {A\, {\bf d}^i \, . \, {\bf d}^i} \; {\bf d}^i $$

2e tentative

La méthode trouvée est bien car elle montre qu'on peut optimiser la descente de gradiant mais le calcul de ${\bf d}^k$ est bien trop lourd. Aussi on va tout recommencer pour trouver une autre facon plus efficace.

Travaillons dans la base des $\nabla J({\bf x}^i)$

On repart de l'équation (0) qui permet de montrer que les $\nabla J({\bf x}^i), i \le k$ forment une bases du sous espace $\bf G_k$. Aussi tout vecteur s'exprime dans cette base et donc

$$ {\bf x}^{k+1} = {\bf x}^k + μ^k \, {\bf d}^k \quad \textrm{avec} \quad {\bf d}^k = - \nabla J({\bf x}^k) + \sum_{i=0}^{k-1} γ^i \, \nabla J({\bf x}^i) $$

On note que ces ${\bf d}^i, i \le k$ forment aussi une base de $\bf G_k$.

L'équation (2) nous dit que $A \, {\bf d}^k \, . \, {\bf d}^i = 0 \quad \forall i < k$, aussi

$$ \begin{align} < A \, {\bf d}^k, {\bf x}^{j+1} - {\bf x}^j > &= 0 \quad \forall j < k \\ < {\bf d}^k, A \, ({\bf x}^{j+1} - {\bf x}^j) > &= 0 \quad \textrm{car A est symétrique} \\ < {\bf d}^k, A \, {\bf x}^{j+1} - {\bf b} - A {\bf x}^j + {\bf b} > &= 0 \\ < {\bf d}^k, \nabla J({\bf x}^{j+1}) - \nabla J({\bf x}^j) > &= 0 \\ < - \nabla J({\bf x}^k) + \sum_{i=0}^{k-1} γ^i \, \nabla J({\bf x}^i) , \nabla J({\bf x}^{j+1}) - \nabla J({\bf x}^j) > &= 0 \quad (3) \\ \end{align} $$

Si j = k-1 alors $$ \begin{align} < - \nabla J({\bf x}^k), \nabla J({\bf x}^k) > + \, γ^{k-1} < \nabla J({\bf x}^{k-1}), -\nabla J({\bf x}^{k-1}) > &= 0 \\ γ^{k-1} = -\frac{< \nabla J({\bf x}^{k}), \nabla J({\bf x}^{k}) >} {< \nabla J({\bf x}^{k-1}), \nabla J({\bf x}^{k-1}) >} \end{align} $$

Si j = k-2 alors $$ \begin{align} γ^{k-1} \, < \nabla J({\bf x}^{k-1}), \nabla J({\bf x}^{k-1}) > + \, γ^{k-2} < \nabla J({\bf x}^{k-2}), -\nabla J({\bf x}^{k-2}) > &= 0 \\ γ^{k-2} = γ^{k-1} \frac{< \nabla J({\bf x}^{k-1}), \nabla J({\bf x}^{k-1}) >} {< \nabla J({\bf x}^{k-2}), \nabla J({\bf x}^{k-2}) >} = \frac{< \nabla J({\bf x}^{k}), \nabla J({\bf x}^{k}) >} {< \nabla J({\bf x}^{k-2}), \nabla J({\bf x}^{k-2}) >} \end{align} $$ et en continuant les calculs, on a $\forall j < k-1$ $$ γ^j = \frac{< \nabla J({\bf x}^{k}), \nabla J({\bf x}^{k}) >} {< \nabla J({\bf x}^{j}), \nabla J({\bf x}^{j}) >} $$

La formule générale de ${\bf d}^k$ est donc $$ \begin{align} {\bf d}^k &= -\nabla J({\bf x}^k) - \frac{< \nabla J({\bf x}^{k}), \nabla J({\bf x}^{k}) >} {< \nabla J({\bf x}^{k-1}), \nabla J({\bf x}^{k-1}) >} \, \nabla J({\bf x}^{k-1}) + \sum_{i=0}^{k-2} \frac{< \nabla J({\bf x}^{k}), \nabla J({\bf x}^{k}) >} {< \nabla J({\bf x}^{i}), \nabla J({\bf x}^{i}) >} \, \nabla J({\bf x}^i) \\ &= -\nabla J({\bf x}^k) + β \left( -\nabla J({\bf x}^{k-1}) + \sum_{i=0}^{k-2} \frac{< \nabla J({\bf x}^{k-1}), \nabla J({\bf x}^{k-1}) >} {< \nabla J({\bf x}^{i}), \nabla J({\bf x}^{i}) >} \, \nabla J({\bf x}^i) \right) \\ &= -\nabla J({\bf x}^k) + β \, {\bf d}^{k-1} \quad \textrm{avec} \quad β = \frac{< \nabla J({\bf x}^{k}), \nabla J({\bf x}^{k}) >} {< \nabla J({\bf x}^{k-1}), \nabla J({\bf x}^{k-1}) >} \end{align} $$

On a donc réussi à exprimer la nouvelle direction seulement en fonction du gradient courant et de la direction précédente.

Nouveau calcul de μ

Le calcul précédent de μ reste valable puisque ce calcul ne dépend pas de la facon d'exprimer ${\bf d}^k$.

$$ µ^k = -\frac{\nabla J({\bf x}^{k}) \, . \, {\bf d}^k} {A \, {\bf d}^k \, . \, {\bf d}^k} \, $$

Avec notre choix de ${\bf d}^k$ cela donne

$$ µ^k = -\frac{<\nabla J({\bf x}^{k}), - \nabla J({\bf x}^{k}) + β \, {\bf d}^{k-1}>} {<A \, {\bf d}^k, {\bf d}^k>} = \frac{<\nabla J({\bf x}^{k}), \nabla J({\bf x}^{k})>} {<A \, {\bf d}^k, {\bf d}^k>} $$ puisque ${\bf d}^{k-1} \perp \nabla J({\bf x}^{k})$.