La méthode du gradient pour résoudre A x = b

Le but de ce TP est de vous laisser avancer tout seul. Reprenez les cours et programmez la méthode du gradient pour résoudre le système matriciel $A {\bf x} = {\bf b}$ avec A symétrique et à diagonale dominante ($a_{ii} > \sum_{k \ne i} |a_{ik}|$).

• Commencez en 2D avec une matrice 2x2, vérifier que le résultat est bon et tracer la courbe de convergence
• Passez en nxn (on montrera que cela marche avec une matrice 9x9)

Il peut être intéressant de normaliser la matrice A pour éviter que les calculs explosent.

def solve_with_gradiant(A, b):
    mu = 0.01

import numpy as np
A = np.random.randint(10, size=(2,2))
A = A + A.T
A += np.diag(A.sum(axis=1))
A

array([[49, 13],
       [13, 13]])

b = A.sum(axis=1)
b

array([62, 26])

solve_with_gradiant(A,b)

Introduire de l'inertie

Introduire de l'inertie dans la méthode du gradient. Que constate-t-on ?

Valeur optimale de µ

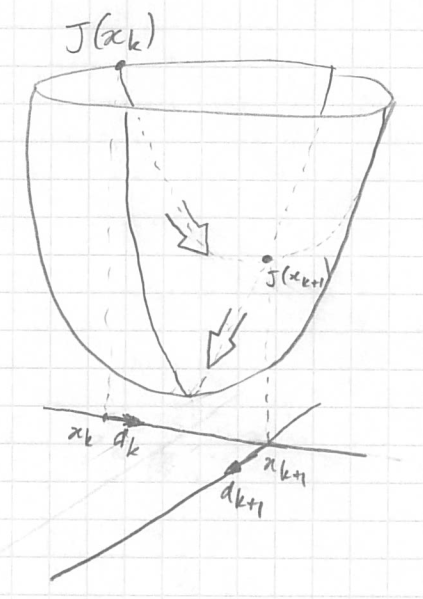
On note que deux directions de pente sucessives sont orthogonales si le point suivant est le minumum dans la direction donnée ($\nabla J ({\bf x}^k$)).

$$\nabla J ({\bf x}^{k+1})^T \; \nabla J ({\bf x}^k) = 0$$

Démonstration

On veut régler µ pour arriver au minimum de J lorsqu'on avance dans la direction $- \nabla J({\bf x}^{k})$. Cela veut dire que la dérivée partielle de $J({\bf x}^{k+1})$ par rapport à µ doit être égale à 0 ou bien en faisant apparaitre µ dans l'équation : $$ \frac{\partial J ({\bf x}^k - µ \; \nabla J ({\bf x}^k))}{\partial µ} = 0 $$ En développant on a $$ \begin{align} \frac{\partial J ({\bf x}^{k+1})}{\partial {\bf x}^{k+1}} \; \frac{\partial {\bf x}^{k+1}}{\partial µ} & = 0 \\ J'({\bf x}^{k+1}) \, . \, (- \nabla J ({\bf x}^k)) & = 0 \\ (A\, {\bf x}^{k+1} - b) \, . \, \nabla J ({\bf x}^k) & = 0 \quad \textrm{puisque A est symétrique}\\ \nabla J ({\bf x}^{k+1}) \, . \, \nabla J ({\bf x}^k) & = 0 \quad \textrm{CQFD} \end{align} $$

En utilisant cette propriété, évaluer la valeur optimale de µ pour atteindre le minimum dans la direction de $\nabla J ({\bf x}^k)$.

Écrire le méthode du gradient avec le calcul du µ optimal à chaque itération pour résoudre $A {\bf x} = {\bf b}$.