Analyse en composantes principales (ACP)¶
import numpy as np
import matplotlib.pyplot as plt
import numpy.linalg as lin
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
np.set_printoptions(precision=3, linewidth=150, suppress=True)
plt.style.use(['seaborn-whitegrid','data/cours.mplstyle'])
import matplotlib
def arrow2D(a,b, color='k', **kargs):
astyle = matplotlib.patches.ArrowStyle("simple", head_length=.8, head_width=.8, tail_width=.1)
plt.plot([a[0],b[0]], [a[1],b[1]] ,visible = False) # to define the visible windows
plt.annotate("", xytext=a, xy=b,
arrowprops=dict(arrowstyle=astyle, shrinkA=0, shrinkB=0, aa=True, color=color, **kargs))
Nuage de points¶
Lorsqu'on a un nuage de points on peut étudier sa forme par une analyse en composantes principales (ACP). Cela revient à chercher les vecteurs propres de la matrice de covariance (ou de corrélation qui est la matrice de covariance normalisée par les écarts types). Ces vecteurs propres nous décrivent le nuage de points.
Pour le vérifier fabriquons un nuage de points avec une corrélation forte entre $x$ et $y$ :
$$ y = 0.2 \, x + 1.45 + U(-1,1) \quad \textrm{avec U la loi uniforme qui simule du bruit.}$$
Cette relation linéaire entre $x$ et $y$ permet de savoir que l'on a :
- une pente de 0.2
- un décalage vertical de 1.45 en x=0
Le but est de voir si, avec seulement le nuage de points, on peut retrouver la corrélation entre $x$ et $y$ malgré le bruit.
$$ y = α x + β$$
N = 50
x = 10 * np.random.rand(N) - 5
nuage = np.array([x, 0.2 * x + 1.45 + (2 * np.random.rand(N) - 1)])
plt.plot(nuage[0], nuage[1], 'x')
plt.title('Un nuage de points')
plt.axis('equal');
Graphiquement on cherche la droite qui minimise la distance entre les points et leur projection sur la droite.
On peut aussi construire la matrice de covariance (cf ci-dessous) et voir que la pente du premier vecteur propre est égale à ce coefficient 0.2 qui relie x à y.
Ensuite la moyenne du nuage de point dans un point de la droite qu'on cherche ce qui fait qu'avec le vecteur directeur qu'est le premier vecteur propre, on a notre droite.
cov = np.cov(nuage.copy())
cov
array([[9.107, 1.925],
[1.925, 0.764]])
Profitons de l'occasion pour rappeler que si une matrice est symétrique alors
- ses valeurs propres sont réelles
- ses vecteurs propres sont orthogonaux
val, vec = lin.eig(cov)
val = val.astype('float') # on convertit puisqu'on sait que ce sont des réels
print("Valeurs propres de la matrice de covariance :", val,"\n")
print("Vecteurs propres de la matrice de covariance :\n", vec)
Valeurs propres de la matrice de covariance : [9.53 0.341] Vecteurs propres de la matrice de covariance : [[ 0.977 -0.215] [ 0.215 0.977]]
/tmp/ipykernel_26870/3419464211.py:2: ComplexWarning: Casting complex values to real discards the imaginary part
val = val.astype('float') # on convertit puisqu'on sait que ce sont des réels
plt.plot(nuage[0], nuage[1], 'x')
arrow2D((0,0), val[0] * vec[:,0], 'r') # vecteur propre multiplié par sa valeur propre
arrow2D((0,0), val[1] * vec[:,1], 'g')
plt.title('Un nuage de points et les vecteurs propres de sa matrice de covariance')
plt.axis('equal');
Vérifions que la pente du premier vecteur propre est proche de 0.2 :
pente = vec[1,0] / vec[0,0]
print("La pente est de", pente, '\n')
moyenne = nuage.mean(axis=1)
print("Le points moyen du nuage est", moyenne)
La pente est de 0.21963615318288862 Le points moyen du nuage est [-0.152 1.327]
eq_droite = lambda x: pente * (x - moyenne[0]) + moyenne[1]
print("Le décalage verticale est de ", eq_droite(0))
plt.plot(nuage[0], nuage[1], 'x')
plt.plot([nuage[0].min(), nuage[0].max()], [eq_droite(nuage[0].min()), eq_droite(nuage[0].max())])
plt.title("Un nuage de points et sa droite d'approximation")
plt.axis('equal');
Le décalage verticale est de 1.360408912029785
print(f'On a donc α = {pente:.3f} et β = {eq_droite(0):.3f} sachant que le nuage a été généré avec 0.2 et 1.45')
On a donc α = 0.220 et β = 1.360 sachant que le nuage a été généré avec 0.2 et 1.45
Matrice de covariance¶
La covariance entre deux jeux de données x et y indique à quel point il sont liés (c.a.d. si la i-ème valeur de y peut se déduire de la i-ème valeur de x ou pas). Si leur covariance est grande en valeur absolue alors ils sont fortement liées, si elle est proche de 0, elles sont soit indépendantes soit liée par une relation plus compliquée qu'une simple relation linéaire.
La covariance mesure la relation linéaire entre 2 variables (cf cette vidéo pour une présentation rapide et complète de la covariance et de ses propriétés).
$$ \textrm{cov}(\textbf{x},\textbf{y}) = \frac{1}{N} \sum_{i=1}^N (x_i - \overline{\textbf{x}}) (y_i - \overline{\textbf{y}}) $$
avec $N$ le nombre de points du nuage, $\overline{\textbf{x}}$ et $\overline{\textbf{y}}$ les moyennes de $\textbf{x}$ et de $\textbf{y}$.
Si on place l'orgine des axes à la moyenne $(\overline{\textbf{x}},\overline{\textbf{y}})$ alors la formule indique que pour avoir corrélation il faut qu'il y ait plus de point dans 2 quadrans diagonalement opposés.
Si à l'inverse on a tire des points aléatoire, donc pas de relation entre x et y, alors on aura des points répartit uniforméments autour de la moyenne donc une covariance nulle. Enfin si toutes les valeurs de $\textbf{y}$ valent une même valeur, alors elles ne dépendent pas de x et $y_i - \overline{\textbf{y}} = 0 \; \forall i$ donc la covariance est nulle.
plt.plot(nuage[0], nuage[1], 'x')
plt.plot([moyenne[0], moyenne[0]], [nuage[1].min(), nuage[1].max()],'k')
plt.plot([nuage[0].min(), nuage[0].max()], [moyenne[1], moyenne[1]],'k')
plt.title('La covariance indique une direction privilégiée et donc plus de points dans les quadrans traversés')
plt.axis('equal');
Ici on voit bien que la grande majorité des points sont dans 2 quadrans opposés, dont nos 2 variables sont liées.
La matrice de covariance exprime toutes les covariances possibles entre les variables. Dans notre cas où le nuage a 2 dimensions, on a :
$$ \textrm{Cov(nuage 2D)} = \begin{bmatrix} \textrm{cov}(\textbf{x},\textbf{x}) & \textrm{cov}(\textbf{x},\textbf{y}) \\ \textrm{cov}(\textbf{y},\textbf{x}) & \textrm{cov}(\textbf{y},\textbf{y}) \\ \end{bmatrix} $$
cov = lambda x,y : np.dot((x - x.mean()), (y - y.mean())) / len(x)
Cov = lambda x,y : np.array([[cov(x,x), cov(x,y)], [cov(y,x), cov(y,y)]])
Cov(nuage[0], nuage[1]) # par défaut Numpy divise par (N-1), avec bias=True il divise par N et donne ce résultat
array([[8.925, 1.887],
[1.887, 0.749]])
Ce résultat montre que x est très liés avec lui-même ce qui est une évidence. Par contre il semble que y soit moins lié avec lui-même. En fait les variation de y sont plus petites (entre 0 et 3 alors que x varie entre -5 et 5) ce qui explique cette plus petite valeur. Le fait que cov(x,y) soit plus grand que cov(y,y) est déjà un indicateur que x et y sont liés.
Le calcul des valeurs et vecteurs propres de la matrice de covariance est encore plus intéressant avec une grande dimension car il fait ressortir lesquelles sont les plus importantes. Ainsi l'exemple de l'article de Wikipédia sur l''analyse en composantes principales sur la pollution de l'eau du Doubs montre que le premier vecteur propre est celui des polluants connus : nitrates (nit), phosphates (pho), ammoniaque (amm) et le second est celui du PH. On notera l'anti-corrélation entre la teneur en oxygène et les polluants.
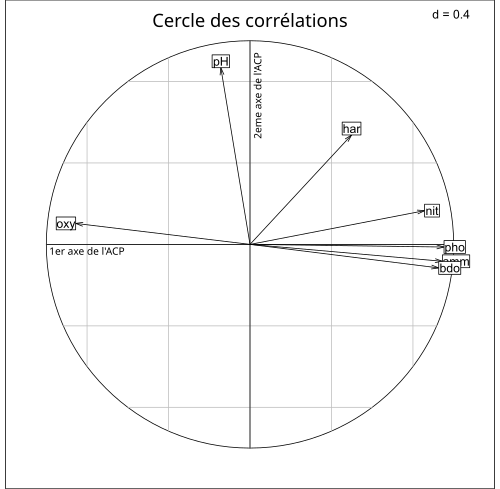
Pour bien comprendre cette figure et voir un cas d'utilisation, je vous invite à regarder cet exemple d'ACP avec Excel.